


Volum av sylinder:
Volum av sylinder:
Volum av sylinder:
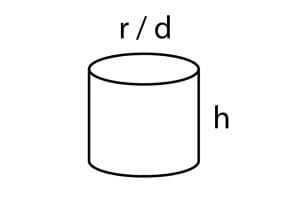

| wdt_ID | Radius (cm) | Volum (cm³) |
|---|---|---|
| 1 | 1 | 31,42 |
| 2 | 2 | 125,66 |
| 3 | 3 | 282,74 |
| 4 | 4 | 502,65 |
| 5 | 5 | 785,40 |
| 6 | 6 | 1.130,97 |
| 7 | 7 | 1.539,38 |
| 8 | 8 | 2.010,62 |
| 9 | 9 | 2.544,69 |
| 10 | 10 | 3.141,59 |
| wdt_ID | Diameter (cm) | Volum (cm³) |
|---|---|---|
| 1 | 2 | 31,42 |
| 2 | 4 | 125,66 |
| 3 | 6 | 282,74 |
| 4 | 8 | 502,65 |
| 5 | 10 | 785,40 |
| 6 | 12 | 1.130,97 |
| 7 | 14 | 1.539,38 |
| 8 | 16 | 2.010,62 |
| 9 | 18 | 2.544,69 |
| 10 | 20 | 3.141,59 |
| wdt_ID | Omkrets (cm) | Volum (cm³) |
|---|---|---|
| 1 | 6,28 | 31,42 |
| 2 | 12,57 | 125,66 |
| 3 | 18,85 | 282,74 |
| 4 | 25,13 | 502,65 |
| 5 | 31,42 | 785,40 |
| 6 | 37,70 | 1.130,97 |
| 7 | 43,98 | 1.539,38 |
| 8 | 50,27 | 2.010,62 |
| 9 | 56,55 | 2.544,69 |
| 10 | 62,83 | 3.141,59 |
